スポンサーリンク
当サイトにはプロモーションが含まれています
※広告で得た収益はすべて利用者さんに還元しています。

ゲーム開発室通信 Vol.4 ～避けゲーのプログラミング解説その④～

ロリポップ公式サイト
ゲーム開発室
スポンサーリンク

第三ステージの障害物の動作編

ご訪問いただき誠にありがとうございます。
今回は第三ステージの障害物の処理について解説いたします。第三ステージは2つの障害物が回転しながら邪魔をしてきます。外側の障害物は大きな円を描きますが速度が速いです。内側の障害物は外側の障害物より遅い速度で回転しています。2つの障害物の軌道から安全地帯を見極めて、障害物をすり抜けられるかがポイントとなるステージです。

実際の「避けゲー」で遊びたい方は以下よりアクセスしてください。

ヒューマンネットのミニゲームのサイトへ

ソースコードはGitHub上にアップしていますので適宜参考にしてください。

第三ステージの制御

第三ステージはenemy4関数とenemy5関数で制御しています。ただし両関数ともコードの内容はほぼ同じです。本来なら1つにまとめた方がいいですね。ブログの後半で2つの関数を1つにまとめる方法についても解説しておりますので最後までお楽しみください。

まずはアクティビティ図とソースコードを見ていきます。処理内容がほぼ同じですので、アクティビティ図はenemy4の方だけ載せています。

コードを見ていただければ分かると思いますが、滑らかな円運動という複雑な動きをしているにも関わらず、コードはとても短いです。こんな短いコードでなぜ円運動のような複雑な動きが可能なのか？それは三角関数を使っているからです。

社会に出ると”中学や高校で習う数学なんてほとんど使わない”と感じてらっしゃる方も多いと思いますが、今回の障害物の動きはまさに”学校で習う三角関数”が大活躍します。

enemy4関数のアクティビティ図
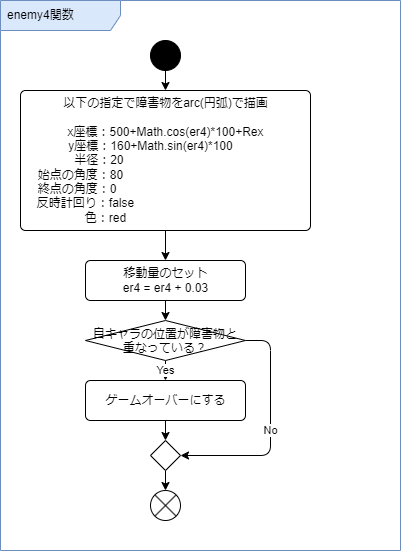
enemy4関数のコード（avoider.jsから抜粋）
function enemy4() {
	//回転しながら円形の障害物の表示
  	ctx.beginPath();
  	ctx.arc(500+Math.cos(er4)*100+Rex, 160+Math.sin(er4)*100, 20, 0, Math.PI*2, false);
  	ctx.fillStyle = "red";
  	ctx.fill();
  	ctx.closePath();
  	er4=er4+0.03;	//回転の移動量のセット
  	if (Math.sqrt((500+Math.cos(er4)*100-x)*(500+Math.cos(er4)*100-x)+(Math.sin(er4)*100)*(Math.sin(er4)*100))<=40) {
   		gameover=true;	//障害物にぶつかったと判定し、ゲームオーバーの判定をセットする
  	}
}
enemy5関数のコード（avoider.jsから抜粋）
function enemy5() {
	//回転しながら円形の障害物の表示
	ctx.beginPath();
  	ctx.arc(500+Math.cos(er5)*250+Rex, 160+Math.sin(er5)*250, 20, 0, Math.PI*2, false);
  	ctx.fillStyle = "red";
  	ctx.fill();
  	ctx.closePath();
	er5=er5+0.05;	//回転の移動量のセット（内側の円より早い速度に設定）
	if (Math.sqrt((500+Math.cos(er5)*250-x)*(500+Math.cos(er5)*250-x)+(Math.sin(er5)*250)*(Math.sin(er5)*250))<=40) {
  		gameover=true;	//障害物にぶつかったと判定し、ゲームオーバーの判定をセットする
	}
}
円弧を描くJavaScriptのAPI
arc(x, y, radius, startAngle, endAngle)
arc(x, y, radius, startAngle, endAngle, counterclockwise)

Canvas 2Dで円、あるいは円弧を描くときはarc()メソッドを使用します。パラメータ（引数）の定義は以下の通りです。

x円弧の中心の水平座標
y円弧の中心の垂直座標
radius円弧の半径（正の数）
startAngle円弧の始まりの角度を、 X 軸の正の方向から時計回りに定められるラジアン角
endAngle円弧の終わりの角度を、 X 軸の正の方向から時計回りに定められるラジアン角
counterclockwise（省略可能）trueの場合、円弧を反時計回りに始まりから終わりの角度に向けて描く
既定値は false（時計回り）
arc()メソッドの詳細
ellipse(x, y, radiusX, radiusY, rotation, startAngle, endAngle [, counterclockwise]);

楕円を描きたい場合はellipse()メソッドが用意されています。

ellipse()メソッドの詳細

円軌道の作り方

第三ステージは2つの障害物が円軌道を描いています。ではどのように円軌道を作っているのか見てみましょう。

ctx.arc(500+Math.cos(er5)*250+Rex, 160+Math.sin(er5)*250, 20, 0,Math.PI*2, false);

arc()メソッドで障害物を描画していますので、arc()メソッドに指定しているx座標（第一引数）とy座標（第二引数）で円軌道を作りだしています。ポイントはx座標にはcos()関数を使っていて、y座標にはsin()関数を使っている点です。なぜそうなるのかを円の性質を表した図で確認しましょう。

円の性質
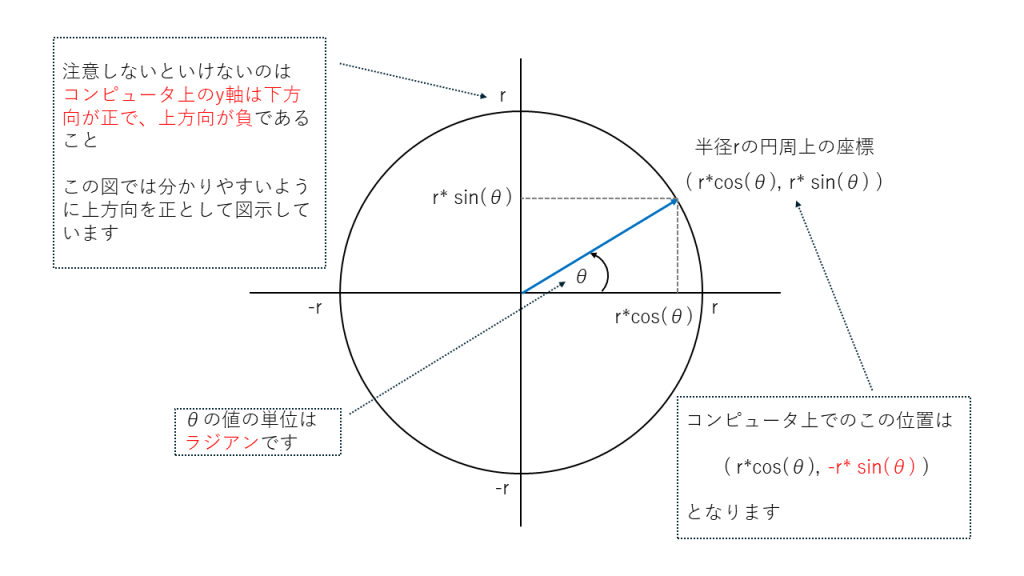
角度はラジアン（弧度）を使用する

一般的に角度を扱うときは90度や180度と表します。これは度数法と呼ばれる角度の扱い方です。ところがプログラミング言語で提供されているAPIのほとんどは度数法ではなくラジアン（弧度法）です。両者は簡単に変換可能ですので、以下の変換式を覚えておくと便利です。

1ラジアン = 180度 / π

「π」は「円周率（パイ）」です。
ラジアンでは180度はπ（≓3.14）です。1周（360度）は2πとなります。arc()メソッドを使って円を描きたいときは引数startAngleを「0」、引数endAngleを「2*Math.PI」と指定すればOKです。

円形の障害物との当たり判定

円形の障害物と自キャラの当たり判定ですが、ここでも中学校で習う数学が活躍します。それは三平方の定理（ピタゴラスの定理）です。三平方の定理を使うと自キャラの座標と障害物である円の中心の座標との間の距離が求まります。ただし、考慮が必要なのは、自キャラも幅と高さを持っているため、どことどことの距離を求めているのかを把握しておかないと、正しい当たり判定にならない点です。今回の自キャラのx座標は自キャラの画像の中心としています。自キャラの大きさは40px ✕ 40pxですので、x座標の位置は左端からも右端からも20pxの位置（画像の中心）となります。さらに障害物である円の半径は20pxですので、当たり判定としては自キャラの座標と障害物の座標との距離が40px以下になれば二つの描画は重なっていると判断できます。

障害物と自キャラの当たり判定のロジック
if (Math.sqrt((500+Math.cos(er4)*100-x)*(500+Math.cos(er4)*100-x)+(Math.sin(er4)*100)*(Math.sin(er4)*100))<=40) {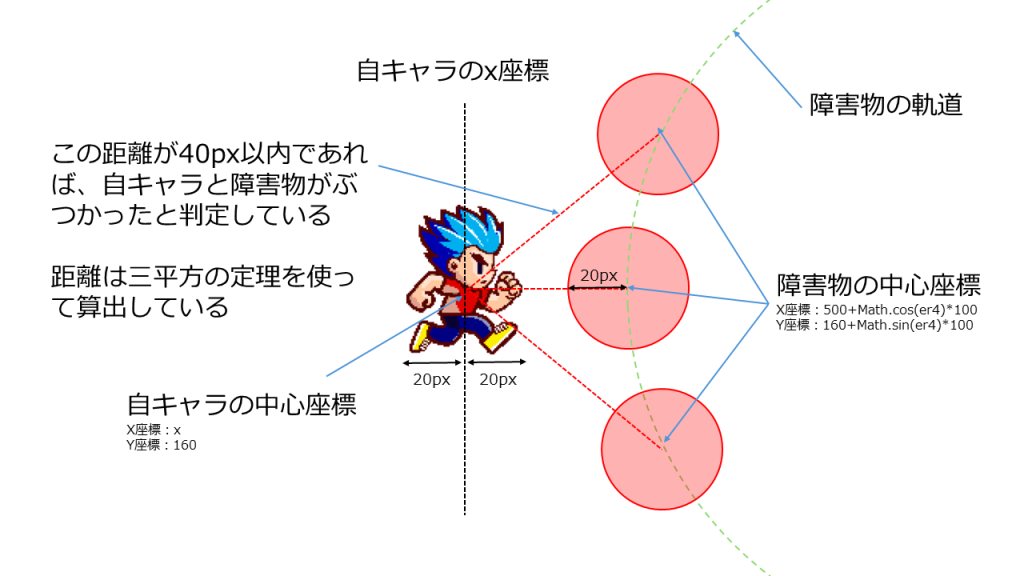

自キャラと障害物との距離の演算式は
√((障害物のx座標 - 自キャラのx座標)2 + (障害物のy座標 - 自キャラのy座標)2)
となりますが、ここでそれぞれのy座標は、

障害物のy座標　：160+Math.sin(er4)*100
自キャラのy座標：160

ですので、「160+Math.sin(er4)*100 - 160」つまり「Math.sin(er4)*100」がy座標の長さとなります。

自キャラのy座標と円の中心のy座標はキャンバス上で同じ位置にいますので、結局円周上のy座標の値が自キャラと障害物とのy軸の距離となりますね。

リファクタリング

プログラムは基本的には目的通りに動いたら、そこで作業は終わりなのですが、一発で完璧なコードを書くことはなかなか難しいです。あーでもない、こーでもないと試行錯誤しながらコードを書いていくと無駄な処理だったり、継ぎ接ぎだらけのコードになってしまいがちです。もう二度とそのコードは見ない、のであればそのままでもいいのですが、システム開発等の仕事ではソースコードはずっと引き継がれていくことが多いですから、出来るだけ分かりやすく無駄のないコードにしておくべきです。一度完成したコードを再度見直して、改善していくことをリファクタリングといいます。日本語で文章を書くときも推敲すると思います。この「推敲」という作業がプログラミングの世界では「リファクタリング」と呼んでいるのです。リファクタリングは原則、次のルールがあります。

リファクタリングとは

プログラムの外部から見た動作を変えずにソースコードの内部構造を整理すること

リファクタリングは内部構造を整理することですから、機能の追加や変更、削除など外から見た動作を変えてはいけません。リファクタリングを行うときはこの原則に従いましょう。

第三ステージの障害物を制御しているenemy4()関数とenemy5()関数は円軌道の半径の大きさと回転速度が違うだけで基本的なロジックは同じ制御となっています。プログラムを書いていると今回のように同じ処理を何度も書いてしまうことがあります。そんなときは出来るだけ処理をまとめた方が効率がよくなります。

今回はenemy4()関数とenemy5()関数を共通化することを例にとってリファクタリングしてみます。その前に処理をまとめたときのメリットとデメリットを上げておきます。

処理の共通化のメリット

  • メンテナンス性が上がる（1カ所修正するだけで済むため）
  • 再利用性が上がる
  • メモリ消費量が減る（プログラム行数が減るため）
  • テスト工数を減らせる

処理の共通化のデメリット

  • 異なる動作をさせにくくなる
  • パラメータ（引数）が増える
  • 共通化し過ぎると返って再利用性が下がる

プログラミングを勉強していると”何度も同じ処理を書くのは悪だ”と教えられることが多いと思いますが、過度の共通化は返って事態を悪化させる場合もあります。メリット・デメリットを考慮しながら、共通化すべきか否かを判断しましょう。

では実際にenemy4()関数とenemy5()関数を共通化していきましょう。まずはお互いの処理についてどこが一緒でどこが異なっているかを確認しましょう。差分は赤字で表示しています。

let er4 = 0;
function enemy4() {
　ctx.beginPath();
　ctx.arc(500+Math.cos(er4)*100+Rex, 160+Math.sin(er4)*100, 20, 0, Math.PI*2, false);
　ctx.fillStyle = "red";
　ctx.fill();
　ctx.closePath();
　er4=er4+0.03;
　if (Math.sqrt((500+Math.cos(er4)*100-x)(500+Math.cos(er4)100-x)+(Math.sin(er4)+100)(Math.sin(er4)*100))<=40) {
　　gameover=true;
　}
}

let er5 = 0;
function enemy5() {
　ctx.beginPath();
　ctx.arc(500+Math.cos(er5)*250+Rex, 160+Math.sin(er5)*250, 20, 0, Math.PI*2, false);
　ctx.fillStyle = "red";
　ctx.fill();
　ctx.closePath();
　er5=er5+0.05;
　if (Math.sqrt((500+Math.cos(er5)*250-x)(500+Math.cos(er5)100-x)+(Math.sin(er5)+100)(Math.sin(er5)*250))<=40) {
　　gameover=true;
　}
}

両関数で異なるところは以下の三つです。

  • 移動量のカウンタである変数er4と変数er5
  • 移動量である0.03と0.05
  • 円軌道の半径である100と250

これら三つの情報が差分になりますので、関数の引数として渡す設計とします。ここで単純に引数として渡せないのが変数のer4とer5です。er4とer5はプリミティブ型の変数です。JavaScriptではC言語のように変数のアドレスを渡せるポインタという使い方が出来ないため、参照渡しが使えません。「変数は分けたい、でも処理は共通化したい」といった場合はどうすれば共通化できるでしょうか？いろいろな方法が考えられると思いますが、1番簡単なのが配列を使う方法です。配列であれば添え字を変えることで、要素を切り替えることができます。他の方法としてはオブジェクト型（参照型）の変数を2つ用意し、引数で参照渡しする方法です。今回は単なる数値を扱いますので、後者のオブジェクト（クラス）を使う方法は少し大げさですので、簡単な配列を使うことにします。

「参照渡し」って何？という方は以下のブログでも解説していますのでご参照ください。

参照型編
参照型編 先輩 今回は新人プログラマにとって分かりにくい「参照型」について見ていきましょう。 新人プログラマ Java言語の型には基本型と参照型の二...
ヒューマンネット上本町センターの...

以下がenemy4()とenemy5を共通化した処理になります。

let er = [0, 0];
function enemy(radius, delta, index) {
　ctx.beginPath();
　ctx.arc(500+Math.cos(er[index])*radius+Rex, 160+Math.sin(er[index])*radius, 20, 0,Math.PI*2, false);
　ctx.fillStyle = "red";
　ctx.fill();
　ctx.closePath();
　er[index]=er[index]+delta;
　if (Math.sqrt((500+Math.cos(er[index])*radius-x)*(500+Math.cos(er[index])*radius-x)+(Math.sin(er[index])*radius)*(Math.sin(er[index])*radius))<=40) {
　　gameover=true;
　}
}

関数の定義を変更しましたので、呼び出し側も変更が必要です。

enemy(100, 0.03, 0);
enemy(250, 0.05, 1);

これでenemy4()とenemy5()の共通化が出来ました。この変更では外部からの見た目は全く変わらず、内部構造だけを変更しました。これがリファクタリングという作業になります。

最後までご覧いただきありがとうございます。

今回は第三ステージの障害物の動きを見ていきました。このステージのポイントは円運動する障害物でした。円運動をプログラミングするのは一見大変そうですが、三角関数を使うと簡単に制御できることがお分かりいただけたと思います。学校で習う数学もときには役に立ちますね。さらに今回はリファクタリングにもチャレンジしました。最初から完璧なコードを書くことは難しいです。コードは完成したあとも”もっと良いコードにできないか？”とか”無駄なコードはないか？”と見直すことが重要です。ぜひ皆さんもそういった視点で過去に書いたコードを見直してみてはいかがでしょうか？

次回は第四ステージの障害物の動きについて見ていきます。第四ステージは障害物に前後に挟まれてしまいます。障害物に触れないように慎重に進んでいきながらクリアを目ざすスレージになっています。第四ステージの障害物はかなり複雑な動きをしますので楽しみにしておいてください。

次回のブログにもお付き合いいただけると嬉しいです。

【PR】FXを始めるなら【DMM FX】！
スポンサーリンク